ピタゴラス勝率とは何か

まず、あらためてピタゴラス勝率と実際の勝率の関係を確認しておきたい。図1は1950-2019年のNPB 球団のシーズン勝率、そしてシーズンのピタゴラス勝率の関係を表したものだ。

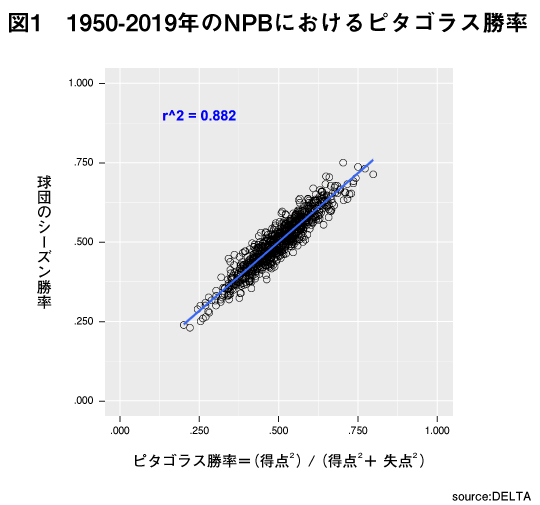
相関係数は0.9393。グラフはきれいな右肩上がりを描いており、ピタゴラス勝率によってチームの勝率をかなり正確に予測できている様子がわかる。

確率を推定するロジスティック回帰モデル

ピタゴラス勝率は得失点で勝率、つまり勝利する確率を推定する統計モデルである。確率推定モデルの代表的な例として、ロジスティック回帰と呼ばれる回帰モデルが挙げられる。ロジスティック回帰は、ある事象が発生したか否か、対象がどのグループに所属するかなど、量で表しにくい質的データの割合を推定する際に用いられる。例えば事象の発生確率PをパラメータWで推定する場合、ロジスティック回帰モデルでは以下の形式で確率Pを推定する。

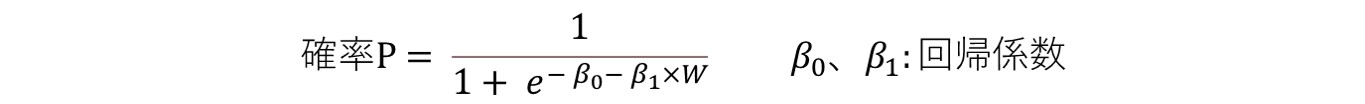
一見複雑な式だが、パラメータWの値にかかわらずPが0から1の範囲で値を取る性質が重要である。この性質は、0から1の範囲に収まる確率を推定する際にうまく機能する。さて、我々が知りたいのは得失点というパラメータと勝率という確率Pの関係であるから、ロジスティック回帰の適用を検討できる。

★★★以下はロジスティック回帰の詳細な解説となる。すでに理解している、あるいは概要のみをつかみたい人は次の★★★まで読み飛ばしてほしい。

ロジスティック回帰を適用する前に、ロジスティック回帰について概略を説明する。ロジスティック回帰では、確率Pのオッズと呼ばれる値について考える。確率Pのオッズとは、ある事象が発生する確率Pと発生しない確率（1－P）の比である。

オッズは0から＋∞の値を取る事を留意しておく。また、オッズの自然対数を対数オッズ、あるいはロジットと呼ぶ。

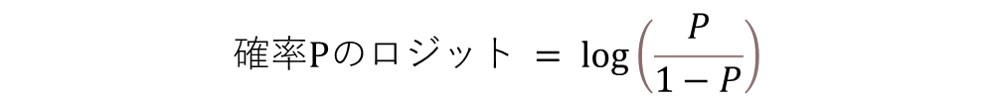
ロジスティック回帰とは、このロジットを特定のパラメータWで推定する手法である。ロジットは-∞から+∞の値を取るため、確率Pを直接求める場合と比較して、かなり広い範囲のパラメータを採用できる。確率Pの推定式は、パラメータWからロジットを推定し、推定したロジットを確率Pの形に変形することで得られる。

ロジット推定の大まかな流れを以下に示そう。確率PのロジットをパラメータWで表すための回帰係数をβ₀ 、β₁とすると、ロジットは以下の形式で表せる。

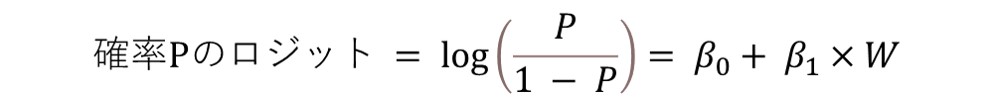
　この式を変形すると、最終的に以下の式を得られる。

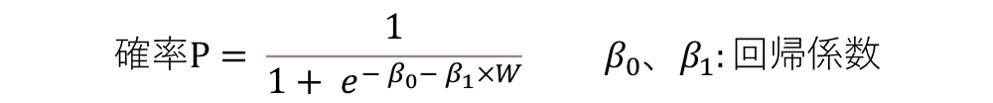
詳細は割愛するが、係数β₀ 、β₁は最尤推定法と呼ばれる手法で決定される。なお、表計算ソフトで計算しやすい最小二乗法でも極めて近いβ₀ 、β₁ を得られるが、最小二乗法の適用は誤差分布など前提条件が必要となる。そのため、最小二乗法による推定と最尤推定法による推定で、結果の解釈が異なる点に注意が必要である。

★★★

ロジスティック回帰モデルを野球に当てはめる

それでは、実際にロジスティック回帰でピタゴラス勝率を導出しよう。はじめに、いくつかの前提を確認する。

①　勝率を得失点で表す妥当性

野球というスポーツでは得点が失点を上回ったチームが勝利する。端的に言えば、得失点のみによって勝敗が決定されるスポーツである。得失点をパラメータとする勝率の推定は、勝敗のルールを踏まえており妥当性があると考えられる。

②　勝率を表すパラメータWの候補

勝率をロジスティック回帰で推定する確率Pとして考えると、勝率Pのオッズは勝利／敗戦 、ロジットはlog（勝利／敗戦）で表せる。

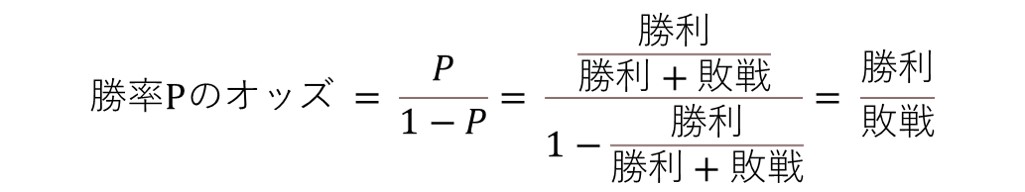
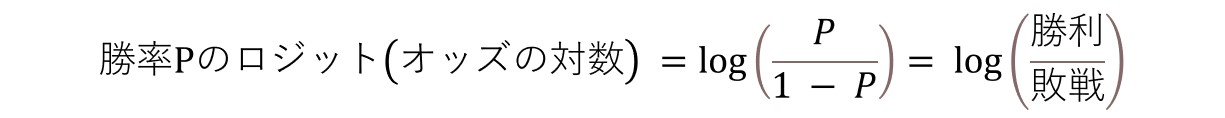
あとは推定に使用するパラメータWさえ決定すれば、ロジスティック回帰で勝率を推定する準備が整う。勝率を推定するパラメータWは、得失点に対して勝率と似た性質を持つパラメータであると好ましい。そのようなパラメータを探すため、得失点に対する勝率の動き（性質）を考えると、以下の性質を得られる。

（1）（2）は勝敗決定ルールから、（3）は勝率の定義から自明である。さて、天下り的だが上記の性質を満足するパラメータとして得点占有率という指標を検討する。得点占有率を以下の式で定義する。

得点占有率は試合の総得点に対する自軍の得点割合を表しており、明らかに（1）（2）（3）の性質を満足している。また、得失点に対する得点占有率と勝率の性質は、オッズやロジット（オッズの対数）についても類似する。

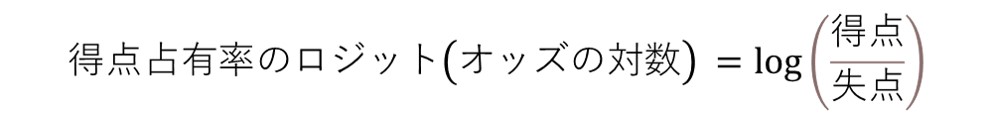
得失点に対する性質を背景に、勝率Pのロジットを推定するパラメータWとして得点占有率のロジットを採用する。これは「勝利／敗戦」をパラメータ「得点／失点」で推定する事にほかならない。

③　ピタゴラス勝率の導出

得点占有率のロジットをパラメータWとして、勝率Pの予測式をロジスティック回帰で導出する。

勝率Pのロジットを得点占有率のロジットWで表すための回帰係数をβ₀ 、β₁とすると、勝率Pのロジットは以下の形式で表せる。この時、β₀ 、β₁ は最尤推定法で決定する。

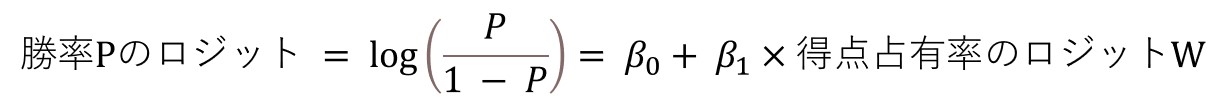
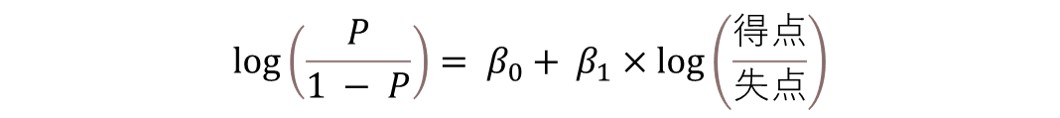
この時、確率Pは以下で表されることを思い出そう。

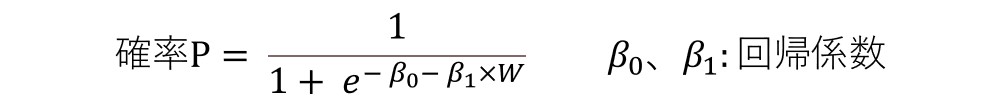
上式でパラメータWにlog（得点／失点）を代入すると、勝率Pの推定モデルを得られる。

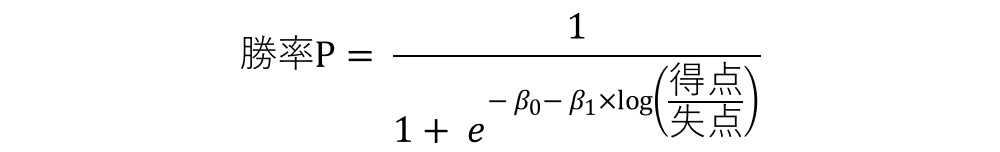
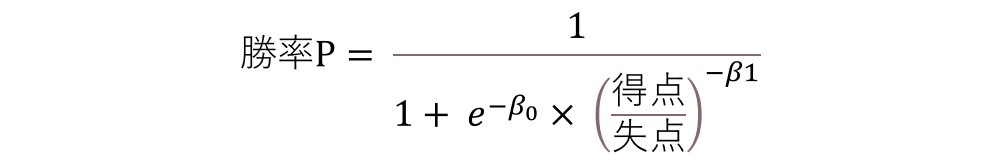
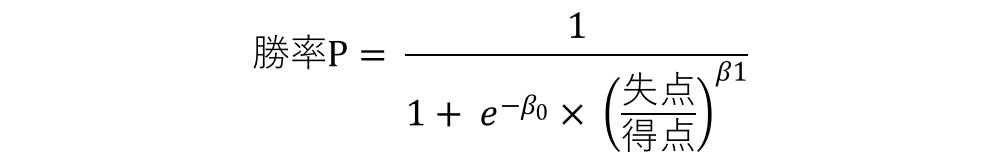
ここでβ₀=0、 β₁=2とした場合、e^-0=1よりBill Jamesが定義した一般的なピタゴラス勝率の形式が得られる。

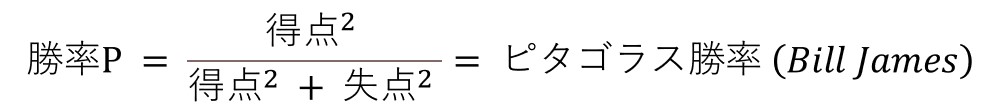
以上の議論により、ピタゴラス勝率の形式がロジスティック回帰によって導出された。実際に、1950-2019年のNPBについて上記モデルで勝率Pのロジスティック回帰を行うと、以下の結果を得られる。

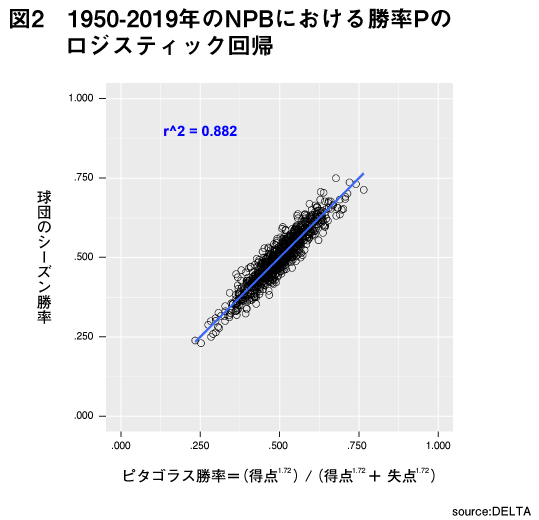
β₀ ~ 0 より e^-β0 ~ 1となることから、Bill Jamesのピタゴラス勝率で暗黙に設定されるβ₀=0という仮定は、NPBにおいても妥当と言えそうだ。β₀= 0とした場合、NPBのピタゴラス勝率は以下で表せる。

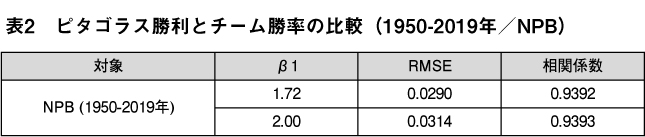
β₀ ~ 0は、得点と失点が等しい場合に勝率が.500前後となる性質を示している。β₁=1.72はBill James式の2.00より小さいが、経験則からMLBではβ₁=1.83、NPBではβ₁=1.72程度がピタゴラス勝率と勝率の誤差を小さくする値とされている。これはロジスティック回帰の結果はほとんど一致しており、異なるプロセスから同等のピタゴラス勝率が導かれる。

ロジスティック回帰で得られたピタゴラス勝率とチーム勝率を比較すると、相関係数0.9392と非常に強い相関を確認できるものの、Bill Jamesのピタゴラス勝率とほとんど同等である。また、二乗平均平方根誤差（RMSE）は β₁=2.00 より β₁=1.72 の方がわずかに小さいものの、両者に大差はない。ピタゴラス勝率で勝率を推定する際、パラメータの細かな大小は推定結果にほとんど影響を与えない事がわかる。ピタゴラス勝率を考える上で重要なのは、得失点で勝率を推定可能という結果である。

野球以外のスポーツにおけるピタゴラス勝率

さて、ピタゴラス勝率の導出では以下のルールを想定していた。

つまり、この条件を満たす競技であれば野球に限らず適用できる可能性がある。多くの点取りゲームで同様の勝利条件が課されているため、ピタゴラス勝率の適用範囲はかなり広そうである。確認のため、野球と同様の手順でサッカーとバスケットボールのピタゴラス勝率を導出した。

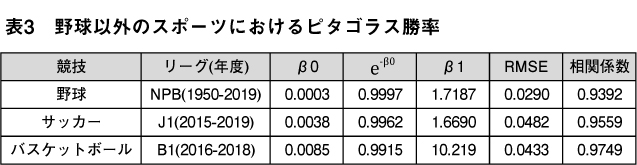
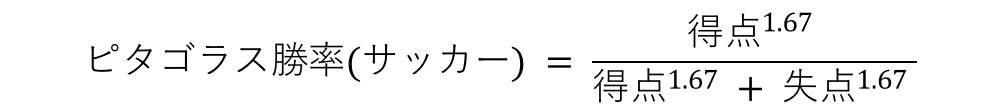
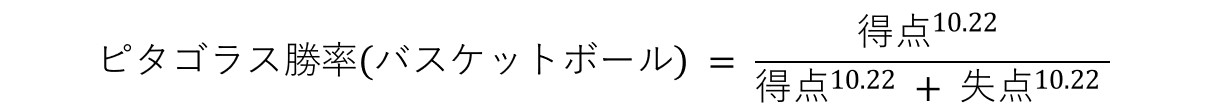
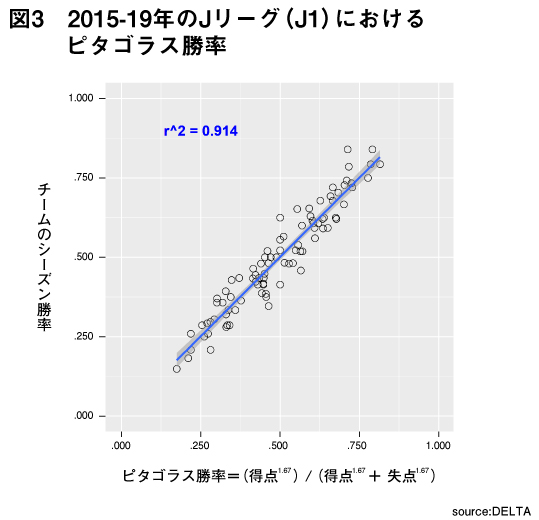
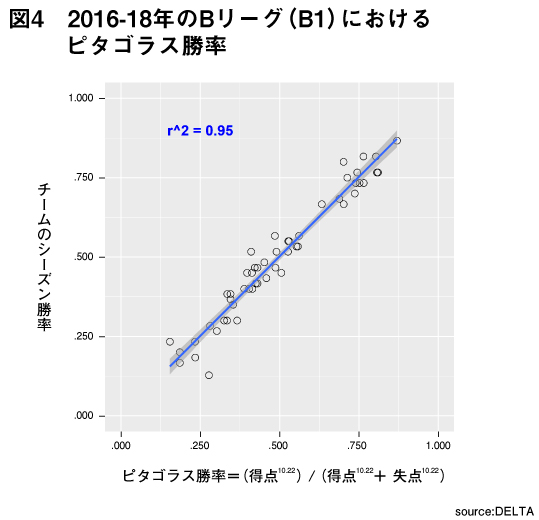
サンプルは野球ほど多くないが、サッカー（J1リーグ）やバスケットボール（B1リーグ）においてもピタゴラス勝率のモデルは非常に良くフィットしている。特にサッカーのピタゴラス勝率は野球に近い係数を得られた。β₀はいずれの競技も0付近であり、基本的に得点と失点の価値は変わらないようだ。

ただし、β₁についてはサッカー＜野球＜バスケットボールとなっており、競技によって差が出ている。この差を可視化するため、各競技における得失点比率=2の場合の標準的なスコアおよび勝利チームのピタゴラス勝率を比較する。

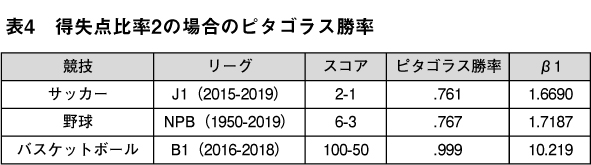
サッカーの2-1と野球の6-3は.750前後のピタゴラス勝率だが、バスケットボールの100-50はピタゴラス勝率.999とほとんど100%である。同じ得失点比率であっても各競技で優勢度は異なり、競技の特性がピタゴラス勝率の指数β₁に表れているようだ。

得点環境によるβ₁の変化

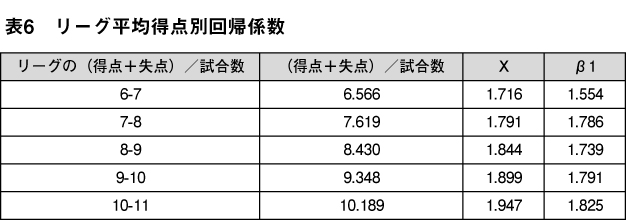
以下は1950-2019年のNPBについて、リーグ平均得点でチームを分類し、ロジスティック回帰によって得られたβ₀ 、β₁ の一覧である。

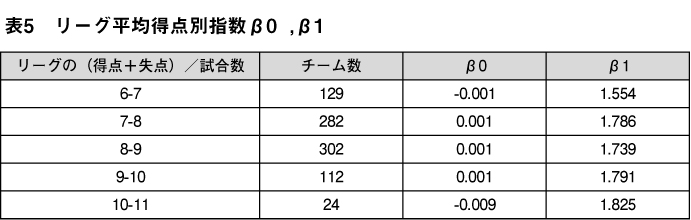
ピタゴラス勝率の指数β₁は概ね平均得点が多いリーグほど大きくなる傾向があるが、7点以上のリーグでは顕著な差は表れていない。MLBの先行研究でも平均得点が多いリーグほどβ₁が大きくなるとされており、PythagenPatと呼ばれる勝率推定式が存在する。

PythagenPatがNPBで適用できる場合、Xとβ₁は概ね一致するはずである。しかし、Xとβ₁の値を比較すると、Xが大きめに算出されている。

β₁をPythagenPatのXと同じ形式

で推定すると、以下の推定式が得られる。

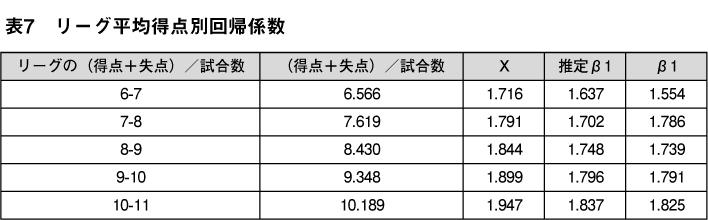
得失点が非常に少ないリーグでは若干誤差が大きいが、PythagenPatのXよりもピタゴラス勝率のパラメータに近い推定値を得られた。よりNPBに適したPythagenPatは以下の形式で表せる。

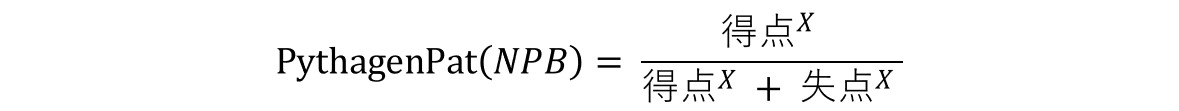
ただし、前述の通りβ₁が多少変化してもピタゴラス勝率の値や精度に大きな差は出ない。重要なのは、得点環境によってピタゴラス勝率のパラメータが変化する性質である。

まとめ

今回はピタゴラス勝率をロジスティック回帰によって導出した。導出過程からわかるとおり、ピタゴラス勝率は「勝利／敗戦」をパラメータ「得点／失点」で推定して得られる勝率である。得点が増えれば勝利に近づき、失点が増えれば敗戦に近づくシンプルな関係性は一見自明だが、その関係は統計的な手法によって導かれる事がわかった。

また、ピタゴラス勝率の形式はほかのスポーツに適用できる事も確認した。ピタゴラス勝率は点取りゲームにおける勝敗の構造を捉えており、いろいろな分野に応用が効く考え方と言える。野球に限らず、各々が興味を持つ分野のピタゴラス勝率について考えるのも一興である。